Hyperbolic (or Simple) Discounting

I was critical of Doyne Farmer in my previous post, and in response I got a message from someone I respect

But I like Farmer's work... solar costs follow Moore's law; and we should value future more (hyperbolic discount rates).

What struck me is that there is an incongruity in associating Moore's Law and Hyperbolic discounting, which I shall explain, and when combined with the first statement points to something more peculiar: do ideas now derive their legitimacy from individuals rather than in relation to each other?

The Moore's Law statement is easier to explain and I assume it comes from this paper (a nice summary was published in Forbes) that investigates the theories

that cost [of production] decreases as a power law of cumulative production [Wright's Law]. An alternative hypothesis is Moore's law, which can be generalized to say that technologies improve exponentially with time.

and that

Our results show that technological progress is forecastable, with the square root of the logarithmic error growing linearly with the forecasting horizon at a typical rate of 2.5% per year. 

I think this final statement exemplifies the gulf between Farmer and myself: he presents technological growth as a matter of (statistical) fact, I see it as one of commercial values (the argument is presented by Deirdre McCloskey, particularly in Bourgeois Dignity).  But this post is not about that.

I suspect the reference to hyperbolic discounting is related to this paper.  Before commenting on Farmer's specific paper I would like to make some comment on the idea of hyperbolic discounting in general.  A hyperbolic discount factor is usually described as follows

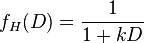
where k is the rate of discounting and D is the maturity (I apologise for the notation I am lifting equation .png from elsewhere to save time).  They are contrasted with exponential discounting factors

.

The statement the hyperbolic discounting implies valuing the future more is a bit naive.  If we fix k then the decline in the exponential discount factor is faster than decline in the hyperbolic discount factor, but this assumes the k in both equations have equivalent meaning, which is not the case - and my undergraduate actuarial students get annoyed with me when suggest (in the context of discrete time derivative pricing) they are.  If we do not assume the rates are the same, we can see we can choose a rate for the exponential that gives the same discount factor as the hyperbolic:

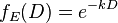Exponential discounting does not imply, a priori, that the future is valued less, the discount rate , k, determines how we value the future.

Farmer points out that hyperbolic functions decrease at a lower rate than exponential functions and so in the limit as time approaches infinity, hyperbolic functions will always value the future more than exponential discounting.  Farmer goes on to suggest that in certain cases of hyperbolic discounting "there is an infinite weight on the far future", this is problematic as if decision making placed infinite weight on the far future we would never consume now, but would have resources available at the end of time when the universe dies.  More technically, these discount functions would contravene the 'transversality condition', which originates in classical mechanics.

Classically in finance, a discount factor is given in terms of hyperbolic discount factor and one uses a D-specific value for k, obtained from the yield-curve.  This gets to the heart of the difference between exponential and hyperbolic discounting; in exponential discounting it is usually assumed that the rate k is constant, and the discounting is time-consistent, where as in hyperbolic discounting the rate k is time-dependent.  This is why the exponential discount function is deemed not to fit Thaler's empirical data, because it is assumed k is fixed, independent of D.

However, it should be noted that the whole field of interest rate models in mathematical finance is concerned with relating the exponential discount rate to the yield curve in order to identify the right discount factor, and in such models it is (generally) assumed that the exponential discount rate is time dependent, and usually stochastic.

To me the discussion of hyperbolic discounting is symptomatic of much of behavioural finance, in that it introduces a sophisticated term into finance for something that has been understood for some time.  My first reaction to hyperbolic discounting was "isn't this just simple (as distinct from compound) discounting", this is a naive but none the less not an unreasonable first approximation. I dislike the adoption of the difficult term "hyperbolic" to re-package the idea that the yield-curve observed in experiments is (peculiarly) decreasing (in itself not a trivial concept) as I see it as "mystifying" finance.  I often associate this process with claims that financial theory is novel.  For example Farmer asserts that exponential discounting was "originally posited by Samuelson (1937) and put on an axiomatic foundation by Koopmans (1960)."  It might come as both a surprise, and a disappointment, to Prof Farmer to learn that the number "e" was first identified by James Bernoulli in 1683,a few years before Newton's  Principia, by considering how a bank account grew as the time between interest payments became infinitesimally small, a year later Leibnitz tackled the problem in the abstract  and arrived at the same answer.  In fact, the problem of Brachistochrone curve, a key step in the development of dynamics, makes a related connection between Bernoulli, Leibnitz, Newton and the transversality condition mentioned above.

The issue I have with hyperbolic discounting is similar to the issue I have with"Prospect Theory"; a key insight of which is that utility functions are S-shaped, this was observed by Friedman and Savage in their 1948 paper The Utility Analysis of Choices Involving Risk (Kahneman and Tversky's paper of 1979, Prospect Theory: An Analysis of Decision Under Risk, has 10 times the citations as Friedman and Savage).  I wonder if this is a reflection of the higher status of the natural sciences over the social sciences: when an economist and a statistician make the observation, it is ignored (partially because it makes the optimisation problem hard), if psychologists make similar observations, admittedly armed with experimental data, it is taken seriously.  I have already discussed similar issues I have with "physics imperialism".  There is also the assumption that because when people are presented with the choices in the experiment choose to value future payoffs peculiarly highly, this is in some way "correct".  Mathematics has a long history of debunking "common sense" because it requires careful thinking.  It is peculiar to value distant payoffs more highly because there is the chance that you die waiting (the experiments usually involve cash payoffs to participants, not public goods).

What perplexes me is that, on the one hand Moore's Law, and the exponential growth of technology, is perceived as reasonable, where as on the other, exponential growth of the much simpler process of money in a bank account, is perceived as unreasonable.  Now some might argue that I miss the essential nature of hyperbolic discounting in associating it with interest accrual, but I would claim this is the essential point.

Financial "behaviour" is that interest is compounded, not simple, and so when discounting I suggest it is more coherent to employ exponential discounting with a non-constant discount rate than try and fit a constant hyperbolic discount rate.  I think this is a preferable approach because it emphasises the dynamic (and contingent) nature of discounting, rather than arguing about the "true" model and its seeking its "true" parameters.

Basically I see the role of academics as making things coherent, identifying the relationship between ideas.  I feel this places me outside the norm, where academic success seems to be measured by coming up with new ideas, even if not new and however problematic they are.  What I find worrying is that there appears to be an emergence of a "cult of personality" in science, where by people express an allegiance to an individual who personifies correct thinking, rather than autonomously challenging authority.  Maybe that's just because I have been too close to the Scottish independence referendum campaign recently and am a bit jaded by it all.