This piece has been posted on the Res Publica think tank Disraeli Room blog.
I recently asked a prominent mathematician who once ran a hedge fund, Doyne Farmer, whether seeking to make a riskless profit was ethical. I don't think he understood the question. Mathematics has always been part of finance but with the re-introduction of derivatives markets in the 1970s and their growth in the nineties, ‘quants’, trained in engineering, physics and mathematics, came to dominate the ‘casino banking’ that is widely criticised. My concern is that the quants are not amenable to questions of morality, and so the problems of finance are going to be difficult to resolve without finding the right way of communicating with the bankers who see themselves as scientists.
I am a mathematician who works on financial problems who became interested in the role of mathematics in the financial crises since 2006. Initially my focus was on explaining why mathematics is so critical to modern banking in response to, for example, the FSA's misplaced assessment, in the Turner Review, that there had been an over-reliance on sophisticated mathematics in the lead up to the crisis (the techniques they discussed were simplistic and not part of mathematics). Subsequent, more authoritative, reviews such as the US Financial Crisis Inquiry Commission and the Parliamentary Commission on Banking Standards removed mathematics from centre stage and replaced it with ethics.
At first sight this re-direction of blame was a relief, but I soon realised it raises a concern: if the problem of finance is one of ethics, what role does mathematics have in its solution? The immediate response is none, but the concern is that if we believe that maths, physics and engineering are concerned with what is, and have nothing to say about what ought to be, we will struggle to convince people trained in the scientific tradition to take commercial corporate morality seriously. The Chartered Institute of Bankers are working on Professional Standards but are struggling to engage with the quants, who operate the casino branch of banking, because the quants believe science is value neutral; it delivers truths beyond morality.
Arguing that ethos and purpose should be placed at the heart of finance misses the point that there is an ethos and purpose at the heart of modern finance. The ethos is based on consequential morality: that an individual seeking a profit has consequential societal benefit, and excesses can be restrained by well-crafted rules. This results in the purpose of finance being any profit within the letter of the law. This ethos presupposes, firstly, that it is possible to calculate consequences and secondly, that restraining regulations can be well crafted. It is a very scientific ethos whose origins can be traced back to Descartes, and comes to us via the British empiricists, Hume and J. S. Mill. It is the ethos that has led to the contemporary study of economics imbuing the student with greed. Many quants would regard the doctrine as being comparable to Darwinian evolution and the Big Bang Theory. This brings to mind Alasdair MacIntyre's ‘disquieting suggestion’ that modern society has completely lost the ability to make moral judgements and I see it as the brick wall that most attempts to reform banking will crash into.
I believe the brick wall can be dismantled relatively easily: by recognising that many of the practices of contemporary finance associated with ‘casino banking’ were widespread before the eighteenth century. Unlike today, they were undertaken in the context not of consequentialist or deontological ethics, but of virtue ethics that focuses on good practice. It might seem surprising that I suggest this is a relatively easy approach. What make it easy is that rather than criticising modern finance on the basis that it is degraded from a mythic golden age of finance, the starting point is the doux-commerce thesis that finance is civilising. Rather than characterising bankers as amoral spivs, they are presented as paragons of rational morality and the approach gives the bankers the opportunity to carry on their activities while, critically, reconstructing their own ethos. I developed this representation in my paper Reciprocity as a Foundation of Financial Economics.
The hurdle this approach needs to cross is that of the dominant ideologies of markets. The market ideology holds that the market mechanism will deliver optimal solutions to society, while anti-market ideology argues that profits are degrading and markets are destructive. The hurdle can be crossed by ignoring both these ideologies and analysing the role that money and markets have played in forming both Western science and democracy. We need to represent markets as centres of communication and deliberation, not as competitive arenas driven by profit maximisation. The clue is in the word forum, which defined both the market place and the political centre of a Roman city.
Thursday, 4 December 2014
Wednesday, 17 September 2014
Hyperbolic (or Simple) Discounting
I was critical of Doyne Farmer in my previous post, and in response I got a message from someone I respect
The Moore's Law statement is easier to explain and I assume it comes from this paper (a nice summary was published in Forbes) that investigates the theories
I suspect the reference to hyperbolic discounting is related to this paper. Before commenting on Farmer's specific paper I would like to make some comment on the idea of hyperbolic discounting in general. A hyperbolic discount factor is usually described as follows
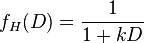
where k is the rate of discounting and D is the maturity (I apologise for the notation I am lifting equation .png from elsewhere to save time). They are contrasted with exponential discounting factors
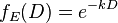 .
.
Exponential discounting does not imply, a priori, that the future is valued less, the discount rate , k, determines how we value the future.
Farmer points out that hyperbolic functions decrease at a lower rate than exponential functions and so in the limit as time approaches infinity, hyperbolic functions will always value the future more than exponential discounting. Farmer goes on to suggest that in certain cases of hyperbolic discounting "there is an infinite weight on the far future", this is problematic as if decision making placed infinite weight on the far future we would never consume now, but would have resources available at the end of time when the universe dies. More technically, these discount functions would contravene the 'transversality condition', which originates in classical mechanics.
Classically in finance, a discount factor is given in terms of hyperbolic discount factor and one uses a D-specific value for k, obtained from the yield-curve. This gets to the heart of the difference between exponential and hyperbolic discounting; in exponential discounting it is usually assumed that the rate k is constant, and the discounting is time-consistent, where as in hyperbolic discounting the rate k is time-dependent. This is why the exponential discount function is deemed not to fit Thaler's empirical data, because it is assumed k is fixed, independent of D.
However, it should be noted that the whole field of interest rate models in mathematical finance is concerned with relating the exponential discount rate to the yield curve in order to identify the right discount factor, and in such models it is (generally) assumed that the exponential discount rate is time dependent, and usually stochastic.
To me the discussion of hyperbolic discounting is symptomatic of much of behavioural finance, in that it introduces a sophisticated term into finance for something that has been understood for some time. My first reaction to hyperbolic discounting was "isn't this just simple (as distinct from compound) discounting", this is a naive but none the less not an unreasonable first approximation. I dislike the adoption of the difficult term "hyperbolic" to re-package the idea that the yield-curve observed in experiments is (peculiarly) decreasing (in itself not a trivial concept) as I see it as "mystifying" finance. I often associate this process with claims that financial theory is novel. For example Farmer asserts that exponential discounting was "originally posited by Samuelson (1937) and put on an axiomatic foundation by Koopmans (1960)." It might come as both a surprise, and a disappointment, to Prof Farmer to learn that the number "e" was first identified by James Bernoulli in 1683,a few years before Newton's Principia, by considering how a bank account grew as the time between interest payments became infinitesimally small, a year later Leibnitz tackled the problem in the abstract and arrived at the same answer. In fact, the problem of Brachistochrone curve, a key step in the development of dynamics, makes a related connection between Bernoulli, Leibnitz, Newton and the transversality condition mentioned above.
The issue I have with hyperbolic discounting is similar to the issue I have with"Prospect Theory"; a key insight of which is that utility functions are S-shaped, this was observed by Friedman and Savage in their 1948 paper The Utility Analysis of Choices Involving Risk (Kahneman and Tversky's paper of 1979, Prospect Theory: An Analysis of Decision Under Risk, has 10 times the citations as Friedman and Savage). I wonder if this is a reflection of the higher status of the natural sciences over the social sciences: when an economist and a statistician make the observation, it is ignored (partially because it makes the optimisation problem hard), if psychologists make similar observations, admittedly armed with experimental data, it is taken seriously. I have already discussed similar issues I have with "physics imperialism". There is also the assumption that because when people are presented with the choices in the experiment choose to value future payoffs peculiarly highly, this is in some way "correct". Mathematics has a long history of debunking "common sense" because it requires careful thinking. It is peculiar to value distant payoffs more highly because there is the chance that you die waiting (the experiments usually involve cash payoffs to participants, not public goods).
What perplexes me is that, on the one hand Moore's Law, and the exponential growth of technology, is perceived as reasonable, where as on the other, exponential growth of the much simpler process of money in a bank account, is perceived as unreasonable. Now some might argue that I miss the essential nature of hyperbolic discounting in associating it with interest accrual, but I would claim this is the essential point.
Financial "behaviour" is that interest is compounded, not simple, and so when discounting I suggest it is more coherent to employ exponential discounting with a non-constant discount rate than try and fit a constant hyperbolic discount rate. I think this is a preferable approach because it emphasises the dynamic (and contingent) nature of discounting, rather than arguing about the "true" model and its seeking its "true" parameters.
Basically I see the role of academics as making things coherent, identifying the relationship between ideas. I feel this places me outside the norm, where academic success seems to be measured by coming up with new ideas, even if not new and however problematic they are. What I find worrying is that there appears to be an emergence of a "cult of personality" in science, where by people express an allegiance to an individual who personifies correct thinking, rather than autonomously challenging authority. Maybe that's just because I have been too close to the Scottish independence referendum campaign recently and am a bit jaded by it all.
But I like Farmer's work... solar costs follow Moore's law; and we should value future more (hyperbolic discount rates).What struck me is that there is an incongruity in associating Moore's Law and Hyperbolic discounting, which I shall explain, and when combined with the first statement points to something more peculiar: do ideas now derive their legitimacy from individuals rather than in relation to each other?
The Moore's Law statement is easier to explain and I assume it comes from this paper (a nice summary was published in Forbes) that investigates the theories
that cost [of production] decreases as a power law of cumulative production [Wright's Law]. An alternative hypothesis is Moore's law, which can be generalized to say that technologies improve exponentially with time.and that
Our results show that technological progress is forecastable, with the square root of the logarithmic error growing linearly with the forecasting horizon at a typical rate of 2.5% per year.I think this final statement exemplifies the gulf between Farmer and myself: he presents technological growth as a matter of (statistical) fact, I see it as one of commercial values (the argument is presented by Deirdre McCloskey, particularly in Bourgeois Dignity). But this post is not about that.
I suspect the reference to hyperbolic discounting is related to this paper. Before commenting on Farmer's specific paper I would like to make some comment on the idea of hyperbolic discounting in general. A hyperbolic discount factor is usually described as follows
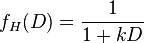
where k is the rate of discounting and D is the maturity (I apologise for the notation I am lifting equation .png from elsewhere to save time). They are contrasted with exponential discounting factors
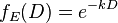 .
.Exponential discounting does not imply, a priori, that the future is valued less, the discount rate , k, determines how we value the future.
Farmer points out that hyperbolic functions decrease at a lower rate than exponential functions and so in the limit as time approaches infinity, hyperbolic functions will always value the future more than exponential discounting. Farmer goes on to suggest that in certain cases of hyperbolic discounting "there is an infinite weight on the far future", this is problematic as if decision making placed infinite weight on the far future we would never consume now, but would have resources available at the end of time when the universe dies. More technically, these discount functions would contravene the 'transversality condition', which originates in classical mechanics.
Classically in finance, a discount factor is given in terms of hyperbolic discount factor and one uses a D-specific value for k, obtained from the yield-curve. This gets to the heart of the difference between exponential and hyperbolic discounting; in exponential discounting it is usually assumed that the rate k is constant, and the discounting is time-consistent, where as in hyperbolic discounting the rate k is time-dependent. This is why the exponential discount function is deemed not to fit Thaler's empirical data, because it is assumed k is fixed, independent of D.
However, it should be noted that the whole field of interest rate models in mathematical finance is concerned with relating the exponential discount rate to the yield curve in order to identify the right discount factor, and in such models it is (generally) assumed that the exponential discount rate is time dependent, and usually stochastic.
To me the discussion of hyperbolic discounting is symptomatic of much of behavioural finance, in that it introduces a sophisticated term into finance for something that has been understood for some time. My first reaction to hyperbolic discounting was "isn't this just simple (as distinct from compound) discounting", this is a naive but none the less not an unreasonable first approximation. I dislike the adoption of the difficult term "hyperbolic" to re-package the idea that the yield-curve observed in experiments is (peculiarly) decreasing (in itself not a trivial concept) as I see it as "mystifying" finance. I often associate this process with claims that financial theory is novel. For example Farmer asserts that exponential discounting was "originally posited by Samuelson (1937) and put on an axiomatic foundation by Koopmans (1960)." It might come as both a surprise, and a disappointment, to Prof Farmer to learn that the number "e" was first identified by James Bernoulli in 1683,a few years before Newton's Principia, by considering how a bank account grew as the time between interest payments became infinitesimally small, a year later Leibnitz tackled the problem in the abstract and arrived at the same answer. In fact, the problem of Brachistochrone curve, a key step in the development of dynamics, makes a related connection between Bernoulli, Leibnitz, Newton and the transversality condition mentioned above.
The issue I have with hyperbolic discounting is similar to the issue I have with"Prospect Theory"; a key insight of which is that utility functions are S-shaped, this was observed by Friedman and Savage in their 1948 paper The Utility Analysis of Choices Involving Risk (Kahneman and Tversky's paper of 1979, Prospect Theory: An Analysis of Decision Under Risk, has 10 times the citations as Friedman and Savage). I wonder if this is a reflection of the higher status of the natural sciences over the social sciences: when an economist and a statistician make the observation, it is ignored (partially because it makes the optimisation problem hard), if psychologists make similar observations, admittedly armed with experimental data, it is taken seriously. I have already discussed similar issues I have with "physics imperialism". There is also the assumption that because when people are presented with the choices in the experiment choose to value future payoffs peculiarly highly, this is in some way "correct". Mathematics has a long history of debunking "common sense" because it requires careful thinking. It is peculiar to value distant payoffs more highly because there is the chance that you die waiting (the experiments usually involve cash payoffs to participants, not public goods).
What perplexes me is that, on the one hand Moore's Law, and the exponential growth of technology, is perceived as reasonable, where as on the other, exponential growth of the much simpler process of money in a bank account, is perceived as unreasonable. Now some might argue that I miss the essential nature of hyperbolic discounting in associating it with interest accrual, but I would claim this is the essential point.
Financial "behaviour" is that interest is compounded, not simple, and so when discounting I suggest it is more coherent to employ exponential discounting with a non-constant discount rate than try and fit a constant hyperbolic discount rate. I think this is a preferable approach because it emphasises the dynamic (and contingent) nature of discounting, rather than arguing about the "true" model and its seeking its "true" parameters.
Basically I see the role of academics as making things coherent, identifying the relationship between ideas. I feel this places me outside the norm, where academic success seems to be measured by coming up with new ideas, even if not new and however problematic they are. What I find worrying is that there appears to be an emergence of a "cult of personality" in science, where by people express an allegiance to an individual who personifies correct thinking, rather than autonomously challenging authority. Maybe that's just because I have been too close to the Scottish independence referendum campaign recently and am a bit jaded by it all.
Friday, 12 September 2014
Economics, Ecology and Ethics
I spent the first part of the week at the eco**2 meeting, sponsored by the British Ecological Society and the LSE's Systemic Risk Centre and exploring the relationship between economics and ecology. I attended because I am in the early stages of a research programme to explore if distinctive financial network topologies emerge out of different commercial cultures, and whether the distinctive topologies are more/less efficient in distributing funds and resilient (robust) in responding to shocks; essentially how financial systems evolve and how the commercial environment influences the financial organisms- the ecology. It was useful as I met for the first time Thomas Lux and Steffano Battiston.
I have a strange connection with ecologists; before becoming an academic I worked for a US oil company in London. In the late 1990s, in response to over a decade of failed exploration, the firm invited John Krebs and Alex Kacelnik to review its approach to exploration based on their experience of optimal foraging strategies of animals. I was the internal project manager. The research was cancelled before the project finished (part of a change in senior staff and a "re-focus") and the two tangible consequences are Oxford Risk and that I list Alex as one of my inspirations to leave industry for academia (along with a choice between a nice redundancy package and PhD in maths or a career in Houston).
One thing that Alex taught me is the sub-optimality of risk-aversion. Some birds need to eat up to 40% of their body weight in a British winter to survive the night, and so their very existence depends on making the right decisions about looking for food. Let's say a bird has 6 hours to find 9 berries and it has two choices:
Alex explained that if the bird has only found five berries after five hours, it is certain to die if it does not switch to the risky strategy, where it has a small chance of finding the 10 berries that will ensure survival. A similar argument applies if the bird has found more than 8 berries after 5 hours - it can afford to take a risk.
The financial interpretation is that only the middle class should be risk averse the rich can afford to gamble, the poor have nothing (substantially) to lose by gambling but there is the small chance they become rich. This is an explanation as to why the poor defy economic 'rationality' in buying lottery tickets, it is actually practically reasonable.
Apart from presenting my own work, my first contribution came in the second plenary when Thomas Lux and Michel Loreau discussed "Important Models in Economics/Ecology". Michel discussed Malthusian catastrophes (possibly in response to a question) and positively contrasted Malthus with Condorcet. This becomes interesting to me, given Condorcet is associated with maths and finance. The moderator asked the audience of mixed "economists" and ecologists if any economist took Malthus seriously, I don't think anyone raised their hand. I felt this left the ecologists with the impression that economists were a bit short sighted. My contribution was the following: Malthus was a Tory cleric worried about the effects of the political changes -the collapse in social hierarchy- in France, where as Condorcet was committed to French Revolutionary principles of equality, brotherhood and freedom. I suggested the reticence of economists to follow Malthus was that his ideas legitimated the liberal policies of the British government during the Irish famine. Restricting growth on the basis of Malthus requires we address the problem of (global) inequality; I question the morality of people with stuff telling people without stuff that they can't have any more stuff. Lord May commented that Malthus was right but the time scale was wrong, I think this is a peculiar view of an empirical scientist: I can point to the problems of the Malthusian catastrophe theory, the theory has yet to be shown to be true. I think the consensus is that famine and pestilence is not an issue of availability of resources but the distribution of resources, what I think economists call the co-ordination problem.
At the end of the day Doyne Farmer captivated his audience by describing his success as a hedge fund quant in the 1990s. I though it a bit odd that the previous evening Lord May had been critical of the type of activities Doyne had been involved with, yet 24 hours later the audience seemed to see the sense of it all. Doyne's story was essentially that he did not believe in the Efficient Markets Hypothesis, and as a skilled mathematician he could go below the economic theory of "first order efficiency" and mine riskless profits in identifying "second order inefficiency". He produced a series of convincing plots, which all seemed to end around 1998. Let's be straight- a priori I am sceptical about Farmer's claims given he claims he built the first wearable computer in the 1970s, where as I believe it was Claude Shannon and Ed Thorpe in the early 1960s. At the end of his presentation a young ecologist asked the question "If you were making money out of these inefficiencies, who was losing money". Farmer skirted round the question, first stating that economics is not a zero-sum game (that is true, but finance IS a zero-sum game) and that the activities of arbitrageurs made markets more efficient (again that is true). What he did not answer was who was losing money.
I then asked Prof Farmer "Is making riskless profits ethical?" My reasons were three-fold.
I have a strange connection with ecologists; before becoming an academic I worked for a US oil company in London. In the late 1990s, in response to over a decade of failed exploration, the firm invited John Krebs and Alex Kacelnik to review its approach to exploration based on their experience of optimal foraging strategies of animals. I was the internal project manager. The research was cancelled before the project finished (part of a change in senior staff and a "re-focus") and the two tangible consequences are Oxford Risk and that I list Alex as one of my inspirations to leave industry for academia (along with a choice between a nice redundancy package and PhD in maths or a career in Houston).
One thing that Alex taught me is the sub-optimality of risk-aversion. Some birds need to eat up to 40% of their body weight in a British winter to survive the night, and so their very existence depends on making the right decisions about looking for food. Let's say a bird has 6 hours to find 9 berries and it has two choices:
- [Play it Safe] The bird stays where it is, where it knows there are berries in the hope of finding a few. The chance of finding one or two berries in the hour is 50:50.
- [Take a Risk] The bird flies off, in the hope of finding berry-bonanza but with a high chance of only finding enough to replace the energy lost in flying. The energy cost of flying is one berry and the chance of only finding the one berry in the new field is 5 in 6, but there is a 1 in 6 chance of finding 10 worms (and getting an excess of 9).
Alex explained that if the bird has only found five berries after five hours, it is certain to die if it does not switch to the risky strategy, where it has a small chance of finding the 10 berries that will ensure survival. A similar argument applies if the bird has found more than 8 berries after 5 hours - it can afford to take a risk.
The financial interpretation is that only the middle class should be risk averse the rich can afford to gamble, the poor have nothing (substantially) to lose by gambling but there is the small chance they become rich. This is an explanation as to why the poor defy economic 'rationality' in buying lottery tickets, it is actually practically reasonable.
Apart from presenting my own work, my first contribution came in the second plenary when Thomas Lux and Michel Loreau discussed "Important Models in Economics/Ecology". Michel discussed Malthusian catastrophes (possibly in response to a question) and positively contrasted Malthus with Condorcet. This becomes interesting to me, given Condorcet is associated with maths and finance. The moderator asked the audience of mixed "economists" and ecologists if any economist took Malthus seriously, I don't think anyone raised their hand. I felt this left the ecologists with the impression that economists were a bit short sighted. My contribution was the following: Malthus was a Tory cleric worried about the effects of the political changes -the collapse in social hierarchy- in France, where as Condorcet was committed to French Revolutionary principles of equality, brotherhood and freedom. I suggested the reticence of economists to follow Malthus was that his ideas legitimated the liberal policies of the British government during the Irish famine. Restricting growth on the basis of Malthus requires we address the problem of (global) inequality; I question the morality of people with stuff telling people without stuff that they can't have any more stuff. Lord May commented that Malthus was right but the time scale was wrong, I think this is a peculiar view of an empirical scientist: I can point to the problems of the Malthusian catastrophe theory, the theory has yet to be shown to be true. I think the consensus is that famine and pestilence is not an issue of availability of resources but the distribution of resources, what I think economists call the co-ordination problem.
At the end of the day Doyne Farmer captivated his audience by describing his success as a hedge fund quant in the 1990s. I though it a bit odd that the previous evening Lord May had been critical of the type of activities Doyne had been involved with, yet 24 hours later the audience seemed to see the sense of it all. Doyne's story was essentially that he did not believe in the Efficient Markets Hypothesis, and as a skilled mathematician he could go below the economic theory of "first order efficiency" and mine riskless profits in identifying "second order inefficiency". He produced a series of convincing plots, which all seemed to end around 1998. Let's be straight- a priori I am sceptical about Farmer's claims given he claims he built the first wearable computer in the 1970s, where as I believe it was Claude Shannon and Ed Thorpe in the early 1960s. At the end of his presentation a young ecologist asked the question "If you were making money out of these inefficiencies, who was losing money". Farmer skirted round the question, first stating that economics is not a zero-sum game (that is true, but finance IS a zero-sum game) and that the activities of arbitrageurs made markets more efficient (again that is true). What he did not answer was who was losing money.
I then asked Prof Farmer "Is making riskless profits ethical?" My reasons were three-fold.
- I felt he had not been sincere in answering the ecologist's question.
- I have argued that the Efficient Markets Hypothesis can bee seen not a statement of fact but one of values: it is a contemporary version of the Scholastic injunction on making riskless profits. Farmer's criticism of the EMH, in my mind, is a criticism of this moral injunction.
- Both the US and UK legislators (in the Financial Crisis Inquiry Commission report of 2011 and the Changing Banking for Good report of 2013) stress the degradation of commercial ethics as a cause of financial crises since 2007.
I do not think I am alone in thinking Doyne did not really understand the question when it was asked. I do not think he really understood what riskless profits means, as opposed to high probability profits, but I also feel he had never considered the ethics of his mathematical modelling (the Professional Standards Board of the Chartered Institute of Banking are interested in my work because they have found it virtually impossible to get the ethics agenda into the "quant" world). I believe the moral vacuum in finance is not endogenous to commerce but has entered the discipline from academia, that is dominated by a strict fact/values dichotomy. Doyne's response was a suggestion that I was evoking some sort of Protestant shaming. I pointed out usury prohibitions were Catholic, the Protestants removed them. But in a sense I was; the previous night Lord May had called for a "professionalisation" of banking, so that those who bought the profession into disrepute could be expelled. The legal, accounting, actuarial, and banking professions all emerged in Presbyterian Scotland, with a tradition of shaming, before Episcopal England. One of the features of contemporary finance is that it is impenetrable for public scrutiny, every thing happens behind closed doors, and so it is difficult to "shame" bankers into probity. If no one asks you if you are behaving ethically, because they cannot see what you are doing, you do not have to worry aebout behaving ethically. Mauss made the point that the difference between science and magic is science is a public activity (like religion) where as magic is purposefully secret.
After the session closed I went to the pub with a couple of ecologists and explained that I asked the question because before the nineteenth century commerce was seen as a civilising (as in supporting civil society) force, not the destructive force we think of today. Shakespeare personified the virtue of charity in Antonio, The Merchant of Venice, something that is inconceivable today. The origins of actuarial science are in the Scottish Ministers' Widows' Fund, a synthesis of Faith, Hope and Charity. Later I was asked "What changed", I took a breath and answered "Darwin".
Starting with Malthus the cooperation metaphor - a key theme in eighteenth century economics, including in Adam Smith - is replaced by the competition metaphor. The economic system shifts from one designed to co-ordinate (equitable) supply and demand to one designed to winnow out the weak and inefficient. I have argued that this reflects society replacing a fear of the uncertain with a concern for scarcity (recall that there were a series of famines in Europe in the second quarter of the nineteenth century), enabled by Laplacian probability reducing distributions to expectations. I do not suggest Darwin was responsible for this shift, but he does personify a general trend that included Mill, Spencer, Galton, Huxley et al., all now seen as pre-eminent figures of English nineteenth century thought. I think the demotion of humans to be "just" another class of animal was a key feature of this period (and this is the opinion of a firm atheist) and was a central result of the nineteenth century biologists.
Something I had not thought of occurred to me on the final day of the workshop. At some point someone had asked if there was the concept of redundancy in economics. I think I answered, but it might only have been in my head, that there is not in economics but there is in finance, where, since the Scottish Ministers' Widows' Fund, at the latest, there has been the issue of reserves. Listening to some of the ecologists I noted that there were repeated references to optimising energy use as a key feature of ecological thought. Similarly a key tool in the physical sciences is minimising energy or maximising entropy. This thought was followed by the thought that physicists often try and see a conceptual relationship between money and energy which seems to completely mis-represent the nature of money.
Sitting in Heathrow's Terminal 5 I thought that the terminal was a masterpiece of efficiency but probably the most inhuman place I had ever been, worse than a nuclear power plant or production line. Waiting for my flight I wondered if the relationship between ecology and economics was more profound that I had ever appreciated, and that the striving for efficiency in economics is in some sense the application of ecological principles. Alfred Marshall is known for both improving the mathematical rigour of economics and advocating the adoption of biological techniques: “the Mecca of the economist lies in economic biology rather than in economic dynamics [i.e. mechanics].” The problems of finance are that a financier's tendency to hold reserves in a stochastic market are challenged by the economist's desire to use capital efficiently, as an animal uses energy efficiently. This is feasible because a Lapacian can reduce a distribution to an expectation and possible because a scientist separates facts and values and sees man as beastly, not virtuous.
I have come to conceive of markets as centres of communicative action reliant on the norms of reciprocity, sincerity and charity. In this formulation mathematics is not used to determine (predict) the truth but as a language to facilitate discourse. I believe, based on sociological studies of the markets, that when market makers offer a price they can be seen as making a claim, which can be challenged by speculators and arbitrageurs, who either accept the claim/price and let it pass, or challenge it by taking the price or offering their own. In this sense mathematical models are used to justify claims, furthermore I believe this practice of using mathematics in justifying claims in finance was adapted in both politics, to deliver democracy, and science: I do not believe in stochastic systems models can be used to predict, only to justify in a discursive process.
This might seem academic and irrelevant, the practical usefulness is that it enables me to identify why practices described by Farmer might be unethical, rather than relying on an instinct that speculation in complex financial instruments just can't be right (where as geo-engineering, genetic modification or nuclear weapons are OK). I aim to show in my research, that such markets can offer growth without creating the inequality that Michel Loreau objected to, but I feel is a consequence of the aim at efficiency that a 'Darwinian' economics demands.
A popular tweet from the meeting was
This might seem academic and irrelevant, the practical usefulness is that it enables me to identify why practices described by Farmer might be unethical, rather than relying on an instinct that speculation in complex financial instruments just can't be right (where as geo-engineering, genetic modification or nuclear weapons are OK). I aim to show in my research, that such markets can offer growth without creating the inequality that Michel Loreau objected to, but I feel is a consequence of the aim at efficiency that a 'Darwinian' economics demands.
A popular tweet from the meeting was
Farmer ends on 'ecological approaches could play important role, but requires abandoning some fundamental assumptions in economics'
— Eco Squared 2014 (@e2c2o2) September 9, 2014
and I ask myself: is this a good thing? Has society been served well by efficiency replacing redundancy in finance and competition metaphors replacing cooperation metaphors in economics? Before ecologists invite economists to abandon some of their fundamental assumptions I would like them to explain how their approaches differ from Darwin's argument articulated in The Descent of Man
My object in this chapter is to shew that there is no fundamental difference between man and the higher mammals in their mental faculties.and that
The great break in the organic chain between man and his nearest allies, which cannot be bridged over by any extinct or living species, has often been advanced as a grave objection to the belief that man is descended from some lower form; ... At some future period, not very distant as measured by centuries, the civilised races of man will almost certainly exterminate, and replace, the savage races throughout the world. At the same time the anthropomorphous apes, as Professor Schaaffhausen has remarked, will no doubt be exterminated. The break between man and his nearest allies will then be wider, for it will intervene between man in a more civilised state, as we may hope, even than the Caucasian, and some ape as low as a baboon, instead of as now between the negro or Australian and the gorilla.In contrast to Darwin, in An Inquiry into the Nature and Causes of the Wealth of Nations Adam Smith argues that humans are distinctive from other animals in the degree to which they are co-operative
Two greyhounds, in running down the same hare, have sometimes the appearance of acting in some sort of concert. Each turns her towards his companion, or endeavours to intercept her when his companion turns her towards himself. This, however, is not the effect of any contract, but of the accidental concurrence of their passions in the same object at that particular timeHumans are different to animals in that they exhibit
the propensity to truck, barter, and exchange one thing for another.Markets are not simply a technical tool to facilitate life, but they capture a key distinction between humans and other animals. I am not convinced that it is progressive to lose the 'civilised' aspect of humanity.
Pragmatism requires me to consider the practical implications of my aim. Someone asked a BBC radio news program what would be the relationship between an independent Scotland and the BBC. As with everything no one knows what will happen post independence (because the nationalists have told us what they want not what they might be able to deliver). The news was not positive for the lover of BBC's Radio 4. It then struck me that much of the independence debate is focused on the unionists pointing out to people who "have"what they might lose in an independent Scotland: jobs, low mortgage rates, large research grants, a stable currency and the BBC. Of course, if you have no job, no mortgage, no money and watch Sky but pay for the BBC, you have nothing to lose but the chance of winning in the nationalist vision of a wealthy and fair society. For me the independence referendum, and the potential for a FN victory in France and the rise of UKIP are the consequences of basing markets on the theory of competition, that accepts the inevitability of extinction of those who can't keep up, rather than social cohesion.
Thursday, 28 August 2014
A short comment on money and independence
During the (now ironically labelled) 'Arab spring' I read Alistair Horne's A Savage War of Peace: Algeria 1954-1962. Reading the introductory chapters describing the state of the French Departments of Algeria in the first half of the twentieth century it struck me that control of the financial system was essential for a political entity to be truly democratic. The context was that after 1848 the Mediterranean coastal region of Algeria had been administered as 3 Departments of France; that is it was integrated into the French National Assembly, unlike British colonies and dominions or the French colonies in West Africa and Indochina. Despite the fact that the political arrangement implied Oran, Algiers and Constantine were on a par with Gironde, Haute-Garonne and Rhone, the financial system of Algeria was controlled from Paris. The result was investment in the 3 departments was made in favour of non-residents rather than the local population, whether pied-noir immigrants or indigenous Arabs. The people did not participate in producing their money; it was alienated from them.
I do not believe that the value of money is based on a commodity, gold or land, or even captures/stores labour. Rather I think that money is a social construction, something that is much harder to explain and therefore harder to believe in. It strikes me that commodity theories of money facilitate the alienation of people from their currency because if money=(gold, land, land+labour) then only the possessors of (gold, land, land+labour) can posses money. In this scheme money ceases to be something to enable social interaction, it becomes something that needs to be accumulated.
I have become interested in financial mechanisms such as peer-to-peer lending and crowdfunding, because I see these as having the potential to re-connect the public with their currency. I am comforted to know that this is emerging as a key theme in Brett Scott's conception of an improved finance. I find it comforting because Brett and I view the problem from very different positions, yet seem to converge on a common understanding. In mathematics, this type of phenomenon is usually taken to mean the common view is likely to be correct.
These ideas have been developed by reading Richard Seaford's excellent Money and the Early Greek Mind: Homer, Philosophy, Tragedy that argues the unique nature of 'Greek civilisation', the basis of Christian and Islamic culture, is public 'ownership' of money. Specifically Greek money emerged out of the communal distribution of sacrificial meat rather than the redistribution of goods from the temple.
Currency has emerged as one of the key topics in the lead up to the Scottish Independence Referendum. I am 1/4 Scots and 3/4 English, but born in Africa (my father was working for the UN); I encourage my 6 yo son to support Scotland in rugby and football; and will be voting against independence. I tend to associate the Yes campaign with men over the age of 40 who blame the ills of Scotland on the closure of the coal, steel and ship-buildling industries orchestrated by English Tories, not on cheap North Sea gas, obsolete manufacturing facilities or innovative Koreans. I believe there is an incoherence between proclaiming green energy but financing yourself by selling oil (the Norwegian model) and I suspect that with an ageing population, declining oil reserves and the prospect of the English fracking to compete with costly North Sea reserves, we are better together.
I know both campaigns are lying to me. The nationalists tell me the only thing that will change post independence is the constitutional arrangement - we will keep the pound, the Queen and the Bank of England, be part of the nice parts of NATO and have exactly the same relationship with Europe. While the unionists promise me that in the event of a No vote Westminster will address all the financial/welfare concerns (without explaining how: I suspect there will be a deal resolving the West Lothian Question in exchange for more financial independence, unless there is a No vote and a Labour government next summer).
I don't think currency is a reason to vote No, if the fundamentals are fine the currency will be fine, but I also don't think the nationalists position on the currency makes any sense. It seems absurd that an independent Scotland would wish to be shackled to the Bank of England, because the people must own their currency to have their freedom. The only explanation I have for the reluctance of the nationalists to opt for the Euro (where the Scots are at an equally disadvantageous position to everyone else outside Germany, rather than being uniquely disadvantaged) is their whole campaign is based on popularity polls rather than coherent policy; this is terrifying and I believe is at the heart of why the polls are so stubborn at the moment. I would be more in favour of an independent Scotland committed to Europe, including the Euro and Schengen (to really annoy the English), than one neither committed to England nor Europe, yet expecting the favours of both. I think it is a shame that the Referendum is essentially a Referendum on SNP policies, not on independence (the emphasis is on getting rid of Trident, not on having the power to get rid of Trident).
Fundamentally I think the whole focus on the currency issue is an expression of the alienation of people from money. If people appreciated money as a social relationship, the significance of the currency would be obvious but the debate would be on the nature of the relationship between England and Scotland, not the embarrassing, unproductive slanging match that, unfortunately, has been the reality of the independence debate and was played out last Monday.
I do not believe that the value of money is based on a commodity, gold or land, or even captures/stores labour. Rather I think that money is a social construction, something that is much harder to explain and therefore harder to believe in. It strikes me that commodity theories of money facilitate the alienation of people from their currency because if money=(gold, land, land+labour) then only the possessors of (gold, land, land+labour) can posses money. In this scheme money ceases to be something to enable social interaction, it becomes something that needs to be accumulated.
I have become interested in financial mechanisms such as peer-to-peer lending and crowdfunding, because I see these as having the potential to re-connect the public with their currency. I am comforted to know that this is emerging as a key theme in Brett Scott's conception of an improved finance. I find it comforting because Brett and I view the problem from very different positions, yet seem to converge on a common understanding. In mathematics, this type of phenomenon is usually taken to mean the common view is likely to be correct.
These ideas have been developed by reading Richard Seaford's excellent Money and the Early Greek Mind: Homer, Philosophy, Tragedy that argues the unique nature of 'Greek civilisation', the basis of Christian and Islamic culture, is public 'ownership' of money. Specifically Greek money emerged out of the communal distribution of sacrificial meat rather than the redistribution of goods from the temple.
Currency has emerged as one of the key topics in the lead up to the Scottish Independence Referendum. I am 1/4 Scots and 3/4 English, but born in Africa (my father was working for the UN); I encourage my 6 yo son to support Scotland in rugby and football; and will be voting against independence. I tend to associate the Yes campaign with men over the age of 40 who blame the ills of Scotland on the closure of the coal, steel and ship-buildling industries orchestrated by English Tories, not on cheap North Sea gas, obsolete manufacturing facilities or innovative Koreans. I believe there is an incoherence between proclaiming green energy but financing yourself by selling oil (the Norwegian model) and I suspect that with an ageing population, declining oil reserves and the prospect of the English fracking to compete with costly North Sea reserves, we are better together.
I know both campaigns are lying to me. The nationalists tell me the only thing that will change post independence is the constitutional arrangement - we will keep the pound, the Queen and the Bank of England, be part of the nice parts of NATO and have exactly the same relationship with Europe. While the unionists promise me that in the event of a No vote Westminster will address all the financial/welfare concerns (without explaining how: I suspect there will be a deal resolving the West Lothian Question in exchange for more financial independence, unless there is a No vote and a Labour government next summer).
I don't think currency is a reason to vote No, if the fundamentals are fine the currency will be fine, but I also don't think the nationalists position on the currency makes any sense. It seems absurd that an independent Scotland would wish to be shackled to the Bank of England, because the people must own their currency to have their freedom. The only explanation I have for the reluctance of the nationalists to opt for the Euro (where the Scots are at an equally disadvantageous position to everyone else outside Germany, rather than being uniquely disadvantaged) is their whole campaign is based on popularity polls rather than coherent policy; this is terrifying and I believe is at the heart of why the polls are so stubborn at the moment. I would be more in favour of an independent Scotland committed to Europe, including the Euro and Schengen (to really annoy the English), than one neither committed to England nor Europe, yet expecting the favours of both. I think it is a shame that the Referendum is essentially a Referendum on SNP policies, not on independence (the emphasis is on getting rid of Trident, not on having the power to get rid of Trident).
Fundamentally I think the whole focus on the currency issue is an expression of the alienation of people from money. If people appreciated money as a social relationship, the significance of the currency would be obvious but the debate would be on the nature of the relationship between England and Scotland, not the embarrassing, unproductive slanging match that, unfortunately, has been the reality of the independence debate and was played out last Monday.
Tuesday, 19 August 2014
Nectar for the gods: how money made Western culture different
I've never really thought that the fact Greek gods lived off nectar and ambrosia was particularly consequential, but having read Richard Seaford's book, Money and the Early Greek Mind: Homer, Philosophy, Tragedy, it seems to have played a fundamental role in the development of Western culture, particularly science, politics and finance.
Unless you are a racist, it is difficult to explain why Western culture delivered wealthy democracies faster than other equally well endowed societies. Since reading Richard Halden's On the shoulders of merchants and Joel Kaye's Economy and nature in the fourteenth century I have been interested in the role that commercial practice played in the emergence of European science, notably how commercial mathematics lead to the mathematisation of science. More recently I have become interested in how commercial practice facilitates the development of democratic politics; that is, a political system that is open to public criticism. In my recent paper on reciprocity I identify connections between finance, science and democracy. My thinking has focused on events in the thirteenth and seventeenth centuries, Seaford's argument takes us right back to the origin of Western thought in the pre-Socratic philosophers and the transormation from beliefs in gods with personalities to abstract, universal conceptions and presents the case that money was central to this transformation. Reading the book reinforces my belief that society should develop a shared conception of what money is in order to support social cohesion
Seaford compares Greek culture principally with the nearby culture of Mesopotamia, with the occasional reference to Egypt. He is currently working on the a comparison of ancient Greek and Indian cultures. This leaves out China, but I feel Mesopotamian beliefs can be regarded as representative of Egyptian, Indian and Chinese beliefs in Seaford's argument.
John Maynard Keynes became obsessed with Babylonian economics before writing his Treatise on Money, noting that the Babylonians employed money as a unit of account such that credit money pre-dated bullion money. This supports state, or chartalist, theories of money as a social construction. Seaford presents a richer argument.
Mesopotamiam societies were, what Seaford labels, redistributive
The Greeks believed that their gods lived on nectar and ambrosia, when they made a sacrifice the smoke of the cooking meat 'honoured' the gods, the cooked meet was distributed equally amongst the community. The fairness of this sharing was fundamental to Greek culture with both the Iliad and the Odyssey resting on problems resulting from unfair (re)distibution [p 44-45]. Seaford emphasises how in Mesopotamian cultures the wealth of the temples was owned by the ruling classes, where as the wealth of the Greek temples was 'owned' by the community
To claim to have identified the origin of money, Seaford must first define what is meant by money. In the context of his work Seaford identifies the characteristics of money as something that:
The basis of the relationship between Greek sacrifices and Greek money is linguistic: the lowest value Greek coin was the obolos, and its took its name from the spits (obelos) that were used to distribute sacrificial food and it is almost certain that the word drachma comes from obeliskon drachmai, 'handfuls of spits' [p 102]. It is harder to explain why spits turned into coin money [6.B] but I think the following passage is significant
Seaford's argument is that Greek philosophy was a consequence of the unique way the Greeks percieved and used money, in everyday transactions. He basis this case on the features of (Greek) money:
Having identified these properties Seaford makes the case for the role of money in the development of Greek philosophy. He starts by criticising the two leading explanations for the emergence of Greek philosophy offered by Vernant and Lloyd. Vernant argues that "In the polis (in contrast to monarchy) citizens are ruled by, and are equal in respect to, impersonal law" while Lloyd emphasises the "freedom of public debate characteristic of the polis: specifically, on the radical revisability of laws, and constitution by the citizens, on their expectation and evaluation of rational justification (evidence and argument), and on the public contexts of competitiveness". Seaford (along with others) challenges these accounts with the questions "when" and "where", arguing that the argument is not supported by when and where Greek philosophy actually emerged.
Unless you are a racist, it is difficult to explain why Western culture delivered wealthy democracies faster than other equally well endowed societies. Since reading Richard Halden's On the shoulders of merchants and Joel Kaye's Economy and nature in the fourteenth century I have been interested in the role that commercial practice played in the emergence of European science, notably how commercial mathematics lead to the mathematisation of science. More recently I have become interested in how commercial practice facilitates the development of democratic politics; that is, a political system that is open to public criticism. In my recent paper on reciprocity I identify connections between finance, science and democracy. My thinking has focused on events in the thirteenth and seventeenth centuries, Seaford's argument takes us right back to the origin of Western thought in the pre-Socratic philosophers and the transormation from beliefs in gods with personalities to abstract, universal conceptions and presents the case that money was central to this transformation. Reading the book reinforces my belief that society should develop a shared conception of what money is in order to support social cohesion
Seaford compares Greek culture principally with the nearby culture of Mesopotamia, with the occasional reference to Egypt. He is currently working on the a comparison of ancient Greek and Indian cultures. This leaves out China, but I feel Mesopotamian beliefs can be regarded as representative of Egyptian, Indian and Chinese beliefs in Seaford's argument.
John Maynard Keynes became obsessed with Babylonian economics before writing his Treatise on Money, noting that the Babylonians employed money as a unit of account such that credit money pre-dated bullion money. This supports state, or chartalist, theories of money as a social construction. Seaford presents a richer argument.
Mesopotamiam societies were, what Seaford labels, redistributive
In the elaborate state systems of Mesopotamia the centralisation had reached an extreme point: redistribution has become the enforced collection of goods and services at a central building (notably temple or palace), where they are used for the upkeep of the central institution, redistribution amongst the population, and for communal functions such as storage against famine, the administration of justice and irrigation [p 69]Mesopotamian religion believed that humans existed to feed the gods and the priests/monarchs were the direct servants of the gods [p 74]. People worked to deliver resources to the centre and the centre re-distributed the resources to the population. Power originated with the gods and could be tapped by the performance of the appropriate ritual, and personal seals (amulets) carried the personal power of the ruling classes.
The Greeks believed that their gods lived on nectar and ambrosia, when they made a sacrifice the smoke of the cooking meat 'honoured' the gods, the cooked meet was distributed equally amongst the community. The fairness of this sharing was fundamental to Greek culture with both the Iliad and the Odyssey resting on problems resulting from unfair (re)distibution [p 44-45]. Seaford emphasises how in Mesopotamian cultures the wealth of the temples was owned by the ruling classes, where as the wealth of the Greek temples was 'owned' by the community
the provision of sacrifice was a matter not just for the sanctuaries but also for the polis. The relationship between the polis and sanctuaries in this matter is hard to disentangle. [p 81]Seaford then goes on to argue that this process of communal, fair, distribution of sacrificial meat, is the origin of 'money'.
To claim to have identified the origin of money, Seaford must first define what is meant by money. In the context of his work Seaford identifies the characteristics of money as something that:
- has the power to meet social obligations (i.e. exchange value, legal compensation, tribute).
- is quantified (i.e. it is not valued for subjective value)
- provides a measure of value (i.e. facilitates transitive relations between objects)
- is generally accepted (i.e. everyone recognises it)
- is exclusively accepted
- carries fiduciarity, (i.e. it is trusted, people have confidence in its immutability as money. Gresham's Law was first described by Aristophanes around 405 BCE in his play The Frogs).
- may be associated with the state.
The basis of the relationship between Greek sacrifices and Greek money is linguistic: the lowest value Greek coin was the obolos, and its took its name from the spits (obelos) that were used to distribute sacrificial food and it is almost certain that the word drachma comes from obeliskon drachmai, 'handfuls of spits' [p 102]. It is harder to explain why spits turned into coin money [6.B] but I think the following passage is significant
socially central sacrificial communality was unknown in the redistributive economies of Egypt and Mesopotamia, where accordingly money functions were performed by mere substances (silver, barley, copper, etc.). Just as entitlement to participate in the Greek sacrificial meal comes to embody participation in the polis as citizen [3.A], so the inheritance of sacrificial distribution in generating collective confidence is reinforced, and then replaced, by the mark stamped on the metal by the polis. The polis, controlling communal sacrifices and the temple treasuries that developed out of the sacrifices, stamps on the metal distributed a symbol that transcends the particularity of specific treasuries and sacrificing groups, establishing the value of the metal, and enhances the identity of the polis among both its own citizens and outsiders [p 113-114].What I find striking in this passage, and the surrounding text, is that money is essentially 'owned' by the community. I believe this is a significant point in the context of the current 'crisis in confidence' of our financial system. In addition, pre-Socratic Greek culture was not blind to the problems of money, they recognised a connection between tyranny and the personal control of money ([p 99], ''Greek tyrants, wealthy in precious metal'' [p 118], [p 121]) and there appear to be problems when wealth becomes personified, as the Mesopotamians personified power. Shortly after reading Seaford's argument I read Brett Scott's piece 'Much soul, very emotion: Why I buy into the cult of Dogecoin' and I sense that the answers to many of Brett's questions could emerge from Seaford's analysis.
Seaford's argument is that Greek philosophy was a consequence of the unique way the Greeks percieved and used money, in everyday transactions. He basis this case on the features of (Greek) money:
- It is homogeneous. While the metal coins might vary in weight and precious metal content coins are made homogeneous by being stamped with the mark of the polis. The homogeneity enables money to be a measure of value. While coin is homogeneous, it also homogenises its users. Kaye [p 74] makes a similar point in the context of scholastic analysis.
- It is impersonal. Because money is homogeneous, it is impersonal; we do not have our favourite coins. This makes money 'promiscuous', we can use it for (almost) anything with anyone.
- Because it is impersonal it is a universal means: "A feast is made for laughter, and wine maketh merry: but money answereth all things".
- It is a universal aim. Sophocles Antigone of around 411 BCE considers "the desire to make profit out of everything" and the Greeks became aware of the problems resulting from intemperate desire for money.
- It is unlimited. Solon (c. 638 BCE – c. 558 BCE) is reported as saying "Of wealth there is no limit that appears to men. For those of us who have the most wealth are eager to double it". Solon lived in a pre-monetised Athens and money only facilitates the acquisition of wealth. the homogeneity and limitlessness of money leads to associations with the ocean.
- It unites and transforms. Theognis (c550 BCE ) argues that wealth persuades the good to turn bad, the ugly become beautiful and so forth. Similarly money can transform corn into meat and "In Aeschylus's image of Ares as 'gold-changer of bodies' the large and personal (bodies) is transformed into the small and impersonal (dust, money). [p 171]"
- It is both concrete and abstract. There is a discrepancy between the value of Greek money and its metallic value, and so it is abstracted from the concrete and becomes ideal and invisible. We think of money in terms of number, not objects. But, this abstraction is dependent on the concrete symbol signifying their value.
- Money is distinct. Its ability to buy everything along with the ability to store, conceal and transport, makes money a unique substance. I observe that it is almost the social equivalent of physical energy.
Having identified these properties Seaford makes the case for the role of money in the development of Greek philosophy. He starts by criticising the two leading explanations for the emergence of Greek philosophy offered by Vernant and Lloyd. Vernant argues that "In the polis (in contrast to monarchy) citizens are ruled by, and are equal in respect to, impersonal law" while Lloyd emphasises the "freedom of public debate characteristic of the polis: specifically, on the radical revisability of laws, and constitution by the citizens, on their expectation and evaluation of rational justification (evidence and argument), and on the public contexts of competitiveness". Seaford (along with others) challenges these accounts with the questions "when" and "where", arguing that the argument is not supported by when and where Greek philosophy actually emerged.
The earliest recorded Greek philosopher is Thales of Miletus (c. 624 – c. 546 BCE), but Seaford does not discuss Thales in detail because our understanding of his thought comes primarily from Aristotle. However, it is worth noting that the earliest coins are from Miletus, Aristotle reports that Thales was rich on account of his commercial expertise and is associated with rejecting the role of anthropomorphic gods in natural phenomena.
Seaford does discuss Thales 'student' Anaximander (and Xenophanes, a fellow Milesian, Parmenides and Heraclitus) at length focusing on the most important aspect of his thought, the principle of to apeiron. The aperion is the primal source of the universe, it is unlimited and encapsulates opposites. Vernat argues that the origin of the aperion is in the 'equilibrium and reciprocity between equals' that was a feature of the polis. But it is difficult for Vernat to associate the process of opposites emerging and being consumed by the aperion to the polis. Seaford offers an explanation in the use of compensation in resolving conflicts and this is only possible in a monetised society, and the first society to be monetised was Miletus. Seaford identifies nine other analogues between money and aperion:
- Both are unlike all other things and unique.
- Each, in a sense, contains all things.
- Both precede and persist all other things (money must exist before it can be used)
- They are both dynamic, in perpetual motion.
- They both surround and steer all things
- They are both impersonal (the aperion is not god-like)
- They are both perceived as being unlimited
- They are both homogenous
- they are both abstract
Seaford then addresses the issue of monism, the belief that the the universe is based on a single essence. This is counter-intuitive in general and would have been particularly problematic in a polytheistic society. Monism is somewhat distinct from monotheism, which pre-date Greek philosophy, in that the essence of the Greek philosophers was impersonal and abstract: unlike Yahweh or Ahura Mazda. This distinguishes Greek thought, ultimately democratic, from other monisms that centre on a supreme monarch. These observations relate to Kaye's discussion [pp 19-36] of the cultural, both political and scientific, impact of the public realisation that the French king Phillip IV had no sovereignty over the market in the first decade of the fourteenth century.
The most exciting section of the book is the discussion of the Pythagoreans. I believe that modern science, in particular mathematics and physics, rest on the foundations laid by Fibonacci and the generations of financial mathematicians that followed him. Seaford takes this viewpoint back to the Pythagoreans (again Seaford avoids Pythagoras himself as he is largely mythic).
The priests of the Pythagorean cult were known as the mathematikoi, which is the Greek for someone who studies and captures the difference between Greek and other, such as Bablyonian, mathematical traditions. In other cultures mathematics was based principally on observation: the Babylonians observed the Pythagorean triples, the Greeks attempted to prove a theorem explaining the observation. In this respect the Greeks can be seen as focusing on theory rather than practice. Seaford argues that this separation has its roots in the Greeks' experience of money. Fundamentally money involves a universally acknowledged quantitative abstraction, and on this basis mathematics can be developed by applying these principles to all phenomena.
In particular Seaford discusses the Pythagorean belief that 'all is number'. Anthropologists widely report that people associate things with numbers, that is they project the characteristic of a thing onto a number. However Seaford argues that the Pythagoreans are being atypical in projecting a number onto a thing. Seaford has a simple explanation for the Pythagorean belief: they are putting a price on everything.
Archytas of Tarentum writes about the impact of the mathematikoi in the early fourth century BCE
The discovery of calculation (logismos) ended civil conflict and increased concord. For when there is calculation there is no unfair advantage, and there is equality, for it is by calculation that we come to agreement in our transactions. [p 269]
I have argued that the concept of reciprocity is embedded in financial economics for precisely these reasons. Richard is not comfortable with this position because he associates reciprocity with 'inalienable' gifts, that is the giving of something that is inseparable from the giver. However I take the broader definition of reciprocity given by Sahlins and am principally concerned with transactions that are temporally separated, and hence intrinsically uncertain.
I see the process Seaford describes: monetisation of society leading to the development of mathematics and scientific thought and the more democratic politics, repeating itself in the medieval period (the twelfth century monetisation, Fibonacci, Albert the Great) and the early modern (Gresham and Stevin followed by Descartes and Newton). I associate this, very public, process as being in opposition to hidden and authoritarian (magical) processes. It is striking to me that the Mesopotamian state looks soviet, at least, and possibly communist while the Greek states, based on individuals speaking and trading freely, is a more Austrian formulation. This was surprising, and challenging, for me, not least because I do not associate Austrian economics with chartalism, but this probably highlights my ignorance.
Reading Richard Seaford's book emphasises to me the importance of developing a shared conception of what money actually is. His argument stresses the importance of money as being something that is shared by and connects a community. In this respect people need to control currency, not banks, and there needs to be more deliberation about what the financial system is about: profit maximisation or social cohesion? It also has implications in the Scottish Independence Referendum: why would an independent Scotland, with a unique identity, want to share a currency with the rest of the UK?
I feel Richard's arguments support my belief that both democracy and science emerge out of commerce: the political centre of the polis was the agora, which was also the market place. The idea that mathematics rests on commerce is anathema to most of my fellow mathematicians, and I doubt that the arguments in Richard's book will have much effect on these positions. Richard notes that most of his colleagues in classics prefer to see the origins of philosophy in written texts and mathematics in music. However I think academics should take these ideas seriously in order to ensure social cohesion.
Friday, 27 June 2014
Academic metrics and market mechanisms: heaven or hell
This post is a draft of my contribution to the 'Independent review of the role of metrics in research assessment' being undertaken by the Higher Education Funding Council of England and Wales (I will think about it over the weekend).
As a mathematician I felt my views were covered in the submission made by Prof David Speigelhalter that he has disseminated. I did not intend to make any further comments until I read the views of Prof Steve Fuller . Specifically, as a Financial Mathematician I believe I can offer some insights on the approach Prof Fuller puts forward.
Prof Fuller’s argument was interesting to me because he starts by considering the clustering of ‘networks’ that some bibliometrics identify; he refers to the clusters as fiefdoms. Since metrics identify these fiefdoms they are useful, he also implies that work that creates connections between fiefdoms/archipelagos should be highly valued. I agree with this observation, and so my main recommendation would be to develop bibliometrics that asses how research facilitates connections on the basis of complex graph theory (as distinct from crude statistics). As a Financial Mathematician I am interested in this area because, since the Financial Crisis, the Bank of England has been encouraging mathematicians to start analysing the financial system as a complex network, with little success that is reflected in the general immaturity of the science (though research is emerging).
My concerns with Prof Fuller’s approach begin with this comment
Since the Financial Crisis there has been increasing interest in what is a “a proper conception of markets” and an emerging (minority) consensus that the current conception is flawed and the Financial Crisis of 2007-2009 and subsequent crises of ethics are the consequences of this flawed conception. One line of thought in this emerging consensus is that the ‘good internal’ to markets is not profit maximisation under scarcity, following from Robbins definition, but the distribution of credit in the presence of uncertainty to support social cohesion, closer to Maynard Keynes conception.
I would suggest that Fuller’s focus on citations is analogous to a naive financier's focus on money. I would argue that the focus of HEFCE should be the less tangible concept of ‘knowledge’, just as a good financier is concerned with ‘credit’. I believe this observation is a markets focussed corollary to the comments made by Meera Sabaratnam.
That is as much as I will say in the submission. There is some context that comes from this response from Brad DeLong on initiatives to change the economics curriculum in the UK. Prof DeLong states
DeLong implies that to challenge mainstream neoclassical economics is to challenge the ideology of possessive individualism. Central to my work is diminishing the role of "max U" in finance and replacing it with reciprocity in the face of uncertainty, which I believe is challenging the ideology of possessive individualism.
I am becoming obsessed with the relationships between finance, science and democracy.
As a mathematician I felt my views were covered in the submission made by Prof David Speigelhalter that he has disseminated. I did not intend to make any further comments until I read the views of Prof Steve Fuller . Specifically, as a Financial Mathematician I believe I can offer some insights on the approach Prof Fuller puts forward.
Prof Fuller’s argument was interesting to me because he starts by considering the clustering of ‘networks’ that some bibliometrics identify; he refers to the clusters as fiefdoms. Since metrics identify these fiefdoms they are useful, he also implies that work that creates connections between fiefdoms/archipelagos should be highly valued. I agree with this observation, and so my main recommendation would be to develop bibliometrics that asses how research facilitates connections on the basis of complex graph theory (as distinct from crude statistics). As a Financial Mathematician I am interested in this area because, since the Financial Crisis, the Bank of England has been encouraging mathematicians to start analysing the financial system as a complex network, with little success that is reflected in the general immaturity of the science (though research is emerging).
My concerns with Prof Fuller’s approach begin with this comment
More specifically, academics should be trained to think about their citations as investments under conditions of scarcity — that is, exactly like a capital resource.and develop with
To be sure, in the end, we will need to admit upfront that the move to citations is a move to integrate a proper conception of markets into the internal dynamics of academic knowledge production.As a financial mathematician who has worked in markets I have a deep commitment to markets but what I wish to highlight in Prof Fuller’s argument (as disseminated) is that it is not clear what is meant by “a proper conception of markets”.
Since the Financial Crisis there has been increasing interest in what is a “a proper conception of markets” and an emerging (minority) consensus that the current conception is flawed and the Financial Crisis of 2007-2009 and subsequent crises of ethics are the consequences of this flawed conception. One line of thought in this emerging consensus is that the ‘good internal’ to markets is not profit maximisation under scarcity, following from Robbins definition, but the distribution of credit in the presence of uncertainty to support social cohesion, closer to Maynard Keynes conception.
I would suggest that Fuller’s focus on citations is analogous to a naive financier's focus on money. I would argue that the focus of HEFCE should be the less tangible concept of ‘knowledge’, just as a good financier is concerned with ‘credit’. I believe this observation is a markets focussed corollary to the comments made by Meera Sabaratnam.
That is as much as I will say in the submission. There is some context that comes from this response from Brad DeLong on initiatives to change the economics curriculum in the UK. Prof DeLong states
I think that modern neoclassical economics is in fine shape as long as it is understood as the ideological and substantive legitimating doctrine of the political theory of possessive individualism.This is really interesting since the term `possessive individualism' was coined by the Canadian political scientist C.B. Macpherson in a critique of the identification of democracy with markets.
DeLong implies that to challenge mainstream neoclassical economics is to challenge the ideology of possessive individualism. Central to my work is diminishing the role of "max U" in finance and replacing it with reciprocity in the face of uncertainty, which I believe is challenging the ideology of possessive individualism.
I am becoming obsessed with the relationships between finance, science and democracy.
Thursday, 19 June 2014
Rethinking the finance curriculum
Emerging in the wake of the Rethinking Economics movement is Rethinking Finance, and it looks as if Rethinking Finance is going to place some emphasis on the finance curriculum, just as Rethinking Economics , as a student organisation, has. @NeilLancastle, one of the organisers of Rethinking Economics asked me for my views on the finance curriculum, with reference to a review published by the CFA Institute Research Foundation.
As a lecturer in finance (derivative markets and pricing to actuarial undergraduates and MSc students) two things are in my mind. Firstly students have little interest in and less conception of the nature of money. I think this is peculiar given they have made a commitment to working in finance which is concerned, principally, with money (OED 7: finance (n); The management of money, esp. public money; the science which concerns itself with the levying and application of revenue in a state, corporation, etc.).
More relevant to the students I work with, who approach finance mathematically, there is virtually no ability to critically reflect on what they are told. This was emphasised a few months ago with our MSc cohort in Quantitative Financial Risk Management, which is notorious for testing maths graduates with qualitative approaches to risk. We arrange for the students to address problems set by business, and this year a problem was set by an asset manager and the question related to the value of active fund management. The students, universally, answered the question on the basis of the guidance and literature that the asset manger provided: they were a series of presentations suitable for a stock pickers' benevolent fund. All the presentations were scholarly weak, but the question the academics, as examiners, had to address was whether it was fair to penalise the students when we do not train them to be critical of published research. In developing mathematicians, the truth is the truth.
What struck me when comparing the CFA's proposals (p 73) with those from a conference sponsored by the Royal Economic Society reported in 2013 was a similarity. The RES highlights
I don't think this lack of clarity about science is a particular feature of the CFA or finance more generally, I think it is a common problem that makes resolving these sorts of issues hard.
Labelling different disciplines as 'science' or 'not science' and be problematic. I tend to use the term 'human sciences' to emphasise an equality of status between history (human), economics (social), biology (natural), physics (physical) and statistics (mathematical). However I do think it is sometimes helpful to use the classical distinctions of episteme, phronesis and techne. The work-place is often associated with techne, the university, especially in the context of research, with episteme. These terms could apply equally well to all disciplines and professional bodies, such as CFA, should be concerned principally with phronesis.
This train of thought might suggest that I think academics do not involve themselves with phronesis, this is not the case. I feel that academics place too much emphasis on episteme at the expense of helping students in developing phronesis. This is demonstrated by graduates leaving university with a sense that they know the truth but completely lacking in practical skills.
These comments encapsulate my criticism of the first part of the CFA report. The second part of the report focuses on six aspects of investment management, namely
A similar issue exists with risk management. Again this is an old practice that has been incorporated in to actuarial science for hundreds of years but is presented as being a modern science.
My work sees EMH as being an expression of justice in exchange, so EHM can be retained even if the focus of finance switches from individual profit maximisation in a competitive arena to reciprocity in support of social cohesion. This work has initiated a switch in my own research from focussing on stochastic control to exploring complex network theory in order to better understand crises.
What links all these six themes is the importance of a historical context. I often remark that for financiaers to justify fat fees they need to convey the impression that they are addressing novel problems. I think if you consider the history of finance you soon come to realise that the problems and technologies are persistent, it is the culture that changes.
Section 3 of the CFA report moves on to consider the teaching of finance in reference to the topics discussed. In section 4 it asks what is missing from the current curriculum and comes up with the seven topics listed earlier.
The first suggestion is the need for more macroeconomics. But what does this mean? Macroeconomics is usually concerned with aggregate parameters - GDP, unemployment, inflation, savings and investment rates, etc. -and the simple relationships between these parameters. The standard models they work with - Aggregate Demand - Aggregate Supply, Investment Saving–Liquidity Preference Money Supply - don't seem that useful to financiers. What I think is more useful is the presentation of money (and finance) as an integral part of a highly connected economic system; the relations between interest rates, exchange rates, prices, demand, supply, confidence, uncertainty.
This observation ties into the second suggestion: the need to take a historical perspective on macro-economics. This should highlight the relationships I mention.
The third suggestion is, to my mind, critical for the CFA syllabus: The History of Finance/Financial Markets. The report lists a number of texts, I would add Geoffrey Poitras' The Early History of Financial Economics, 1478-1776: From Commercial Arithmetic to Life Annuities and Joint Stocks. I would also support strongly William Goetzmann's comments that
I have been told that there is a trend in business schools (and the like) to shift from focusing on a narrow definition of finance to evolving into research/teaching establishments that place finance at the centre of an multi-disciplinary constellation. I understand this is the ethos at Copenhagen and Vienna. In this setting it is hard to see how behavioural finance does not become integral to finance as a whole.
From this starting point, Behavioural Finance follows as well as the Ethics issue. I must admit that I feel the CFA is weak on ethics, its Code of Conduct appears to me nothing more than "don't break the law". Ethics is much more than this. The Governor of the Bank of England recently highlighted the issue in a speech where it is pointed out that , in the past
Finally, since 2007 I have perceived a convergence of asset and risk management practices, locally this is characterised by Standard Life's GARS fund. My suggestion to the CFA is to re-structure "Modern Portfolio Theory" as "Risk Management" with Markowitz, and its successors, being one approach where risk is managed by minimising variance of returns.
In summary, my syllabus structure would be
As a lecturer in finance (derivative markets and pricing to actuarial undergraduates and MSc students) two things are in my mind. Firstly students have little interest in and less conception of the nature of money. I think this is peculiar given they have made a commitment to working in finance which is concerned, principally, with money (OED 7: finance (n); The management of money, esp. public money; the science which concerns itself with the levying and application of revenue in a state, corporation, etc.).
More relevant to the students I work with, who approach finance mathematically, there is virtually no ability to critically reflect on what they are told. This was emphasised a few months ago with our MSc cohort in Quantitative Financial Risk Management, which is notorious for testing maths graduates with qualitative approaches to risk. We arrange for the students to address problems set by business, and this year a problem was set by an asset manager and the question related to the value of active fund management. The students, universally, answered the question on the basis of the guidance and literature that the asset manger provided: they were a series of presentations suitable for a stock pickers' benevolent fund. All the presentations were scholarly weak, but the question the academics, as examiners, had to address was whether it was fair to penalise the students when we do not train them to be critical of published research. In developing mathematicians, the truth is the truth.
What struck me when comparing the CFA's proposals (p 73) with those from a conference sponsored by the Royal Economic Society reported in 2013 was a similarity. The RES highlights
There was broad agreement that students need:where as the CFA
- Greater awareness of economic history and current real-world context;
- Better practical data-handling skills;
- Greater ability to communicate economics to non-specialists;
- More understanding of the limitations of modelling and current economic methodology;
- A more pluralistic approach to economics;
- A combination of deductive and inductive reasoning.
asked sources what subjects they believed should be reinforced in or added to the curriculum. ..., as follows:The key overlap seems to me to be in
• macroeconomics,
• a historical perspective on macroeconomics,
• the history of financial markets and economic history,
• behavioral finance,
• statistics beyond the use of the normal distribution,
• risk management, and
• ethics.
- a historical perspective [this would lead to]
- pluralism
- practical tools
- a synthesis of facts with values
Is our “science” merely an idealized rational construction that ignores market realities? If so, exactly what should we be teaching students of finance whose objective is to manage other people’s money? Is an alternative science based on observations available (or in progress)? Or does our current knowledge of economics and finance have to be removed from the realm of science altogether and placed on a par with the social sciences? (my emphasis)I think what this highlights is a lack of clarity over what is meant by 'science' (in what sense are social sciences removed from the realm of science?). Because there is this lack of clarity, I think it is difficult how to answer the questions posed.
I don't think this lack of clarity about science is a particular feature of the CFA or finance more generally, I think it is a common problem that makes resolving these sorts of issues hard.
Labelling different disciplines as 'science' or 'not science' and be problematic. I tend to use the term 'human sciences' to emphasise an equality of status between history (human), economics (social), biology (natural), physics (physical) and statistics (mathematical). However I do think it is sometimes helpful to use the classical distinctions of episteme, phronesis and techne. The work-place is often associated with techne, the university, especially in the context of research, with episteme. These terms could apply equally well to all disciplines and professional bodies, such as CFA, should be concerned principally with phronesis.
This train of thought might suggest that I think academics do not involve themselves with phronesis, this is not the case. I feel that academics place too much emphasis on episteme at the expense of helping students in developing phronesis. This is demonstrated by graduates leaving university with a sense that they know the truth but completely lacking in practical skills.
These comments encapsulate my criticism of the first part of the CFA report. The second part of the report focuses on six aspects of investment management, namely
- diversification,
- optimization-diversification formalized,
- the CAPM and similar models,
- the efficient market hypothesis,
- risk measurement and risk management, and
- crises.
A similar issue exists with risk management. Again this is an old practice that has been incorporated in to actuarial science for hundreds of years but is presented as being a modern science.
My work sees EMH as being an expression of justice in exchange, so EHM can be retained even if the focus of finance switches from individual profit maximisation in a competitive arena to reciprocity in support of social cohesion. This work has initiated a switch in my own research from focussing on stochastic control to exploring complex network theory in order to better understand crises.
What links all these six themes is the importance of a historical context. I often remark that for financiaers to justify fat fees they need to convey the impression that they are addressing novel problems. I think if you consider the history of finance you soon come to realise that the problems and technologies are persistent, it is the culture that changes.
Section 3 of the CFA report moves on to consider the teaching of finance in reference to the topics discussed. In section 4 it asks what is missing from the current curriculum and comes up with the seven topics listed earlier.
The first suggestion is the need for more macroeconomics. But what does this mean? Macroeconomics is usually concerned with aggregate parameters - GDP, unemployment, inflation, savings and investment rates, etc. -and the simple relationships between these parameters. The standard models they work with - Aggregate Demand - Aggregate Supply, Investment Saving–Liquidity Preference Money Supply - don't seem that useful to financiers. What I think is more useful is the presentation of money (and finance) as an integral part of a highly connected economic system; the relations between interest rates, exchange rates, prices, demand, supply, confidence, uncertainty.
This observation ties into the second suggestion: the need to take a historical perspective on macro-economics. This should highlight the relationships I mention.
The third suggestion is, to my mind, critical for the CFA syllabus: The History of Finance/Financial Markets. The report lists a number of texts, I would add Geoffrey Poitras' The Early History of Financial Economics, 1478-1776: From Commercial Arithmetic to Life Annuities and Joint Stocks. I would also support strongly William Goetzmann's comments that
Studying the how and why of financial institutions, markets and instruments forces us to understand modern finance in the broader context of human lives. It provides a framework for understanding how finance can make the world better and what kinds of possibilities and problems can emerge.I think this: disseminating the role finance has played in stimulating the development of science and democracy; should be a core priority of the CFA, as the principle professional body. This is an emphatic statement but having met Richard Seaford recently, who argues that the origins of Greek philosophy are in money, combined with my knowledge of the impact of finance on European thought in the thirteenth and seventeenth century, I think this is an important story untold, to the detriment of financiers and their practice.
I have been told that there is a trend in business schools (and the like) to shift from focusing on a narrow definition of finance to evolving into research/teaching establishments that place finance at the centre of an multi-disciplinary constellation. I understand this is the ethos at Copenhagen and Vienna. In this setting it is hard to see how behavioural finance does not become integral to finance as a whole.
From this starting point, Behavioural Finance follows as well as the Ethics issue. I must admit that I feel the CFA is weak on ethics, its Code of Conduct appears to me nothing more than "don't break the law". Ethics is much more than this. The Governor of the Bank of England recently highlighted the issue in a speech where it is pointed out that , in the past
Bank leaders created cultures around a simple principle: if it’s legal and others are doing it, we should do it too if it makes money. It didn’t matter if it as the right thing to do for the customer, community or countryThe rational approach to ethics is to place it in a cultural context, this is only really feasible if the theory of finance is placed in a cultural context.
Finally, since 2007 I have perceived a convergence of asset and risk management practices, locally this is characterised by Standard Life's GARS fund. My suggestion to the CFA is to re-structure "Modern Portfolio Theory" as "Risk Management" with Markowitz, and its successors, being one approach where risk is managed by minimising variance of returns.
In summary, my syllabus structure would be
- The nature of money (macroeconomics and more)
- The purpose of finance (history and ethics)
- The practice of finance (behavioural, risk and asset management)
- Tools and techniques (optimisation, statistics)
Friday, 13 June 2014
Reciprocity and the difference between usury and interest
At the IASH meeting on the Human-Business interface I attended last week, Michael Northcott discussed the relationship between capitalism and sustainability. Michael is an authority on both subjects, having written on environmental ethics and debt. At the end of Michael's presentation I made the point that theologians distinguished interest ad usury in the past, a distinction that was missing in Michael's discussion.
Usury derives from the Latin usus, meaning 'use', and referred to the charging of a fee for the use of money. Interest comes from the Latin interesse, meaning 'compensation for loss', and originated, in the Roman legal codes as the fee someone was paid if they suffered a loss as a result of a contract being broken. So a lender could charge interest to compensate for a loss, but they could not make a gain by lending.
It is easier to understand this distinction with a simple example. A farmer lends a cow to their cousin for a year. In the normal course of events, the cow would give birth to a calf and the cousin would gain the benefit of the cow's milk. At the end of the loan, the farmer could expect the cow and the calf to be returned. The interest rate is 100%, but it is an interest since the farmer, if they had not lent the cow to their cousin, would have expected to end the year with a cow and a calf. Similarly, if the farmer lent out grain, they could expect to get the loan plus a premium on the basis that their cousin planted the grain, he would reap a harvest far greater than the sum lent.
Because money is 'barren', unlike land or labour it could not 'produce' anything. As a result, money can have no intrinsic value, other than its use to facilitate exchange, and so charging for the lending of money is essentially selling something that has no value. Thomas Aquinas argued that
In theory, this is all very clear, in practice there was still the question of where the dividing line between usury and interest was and almost everyone who was handling money was looking to charge as much interest as was permissible.
Around 1236, an English professor of canon (church) law, Alanus Anglicus, argued that usury did not exist if the future price of the good was uncertain in the mind of the merchant. These theories became established in the medieval legal system between 1246 and 1253 by Pope Innocent IV, a former professor of law at Bologna. Not only could a merchant adjust the 'just price' to cover their labour and expenses, but also they could also adjust the price to take into account the risk they bore, called an aleatory contract, from the Latin word alea for chance. In establishing this principle, a Catholic jurist initiated the scientific study of financial risk.
Today, financial economics models interest through a force of interest, r, and so the value of a loan of X0 at time t = 0 would be repaid by an amount XT given by
Usury derives from the Latin usus, meaning 'use', and referred to the charging of a fee for the use of money. Interest comes from the Latin interesse, meaning 'compensation for loss', and originated, in the Roman legal codes as the fee someone was paid if they suffered a loss as a result of a contract being broken. So a lender could charge interest to compensate for a loss, but they could not make a gain by lending.
It is easier to understand this distinction with a simple example. A farmer lends a cow to their cousin for a year. In the normal course of events, the cow would give birth to a calf and the cousin would gain the benefit of the cow's milk. At the end of the loan, the farmer could expect the cow and the calf to be returned. The interest rate is 100%, but it is an interest since the farmer, if they had not lent the cow to their cousin, would have expected to end the year with a cow and a calf. Similarly, if the farmer lent out grain, they could expect to get the loan plus a premium on the basis that their cousin planted the grain, he would reap a harvest far greater than the sum lent.
Because money is 'barren', unlike land or labour it could not 'produce' anything. As a result, money can have no intrinsic value, other than its use to facilitate exchange, and so charging for the lending of money is essentially selling something that has no value. Thomas Aquinas argued that
To take usury for money lent is unjust in itself, because this is to sell what does not exist, and this evidently leads to inequality which is contrary to justice.So, usury contradicts 'natural law'. Even if you could convince the canon lawyers that you were, in fact, selling something that did exist, the theologians might argue that usury was an affront to God because, since money was barren, the usurer was charging for time, and "time was God's exclusive property''.
In theory, this is all very clear, in practice there was still the question of where the dividing line between usury and interest was and almost everyone who was handling money was looking to charge as much interest as was permissible.
Around 1236, an English professor of canon (church) law, Alanus Anglicus, argued that usury did not exist if the future price of the good was uncertain in the mind of the merchant. These theories became established in the medieval legal system between 1246 and 1253 by Pope Innocent IV, a former professor of law at Bologna. Not only could a merchant adjust the 'just price' to cover their labour and expenses, but also they could also adjust the price to take into account the risk they bore, called an aleatory contract, from the Latin word alea for chance. In establishing this principle, a Catholic jurist initiated the scientific study of financial risk.
Today, financial economics models interest through a force of interest, r, and so the value of a loan of X0 at time t = 0 would be repaid by an amount XT given by
This implies that the
repayment amount Xt is the solution to the
most basic differential equation,
that is, Xt grows at a
constant rate r. This links to Piketty’s thesis that
capitalism induces inequality because r, the return on money,
is greater than g the growth rate of the economy. This is
conventional economic theory.
I argue that at the heart of financial economics is not growth but reciprocity, so how do I account for interest?
In 1837 Poisson wrote Recherches sur la probabilité des jugements en matiére criminelle et en matiére civile (‘Research on the Probability of Judgments in Criminal and Civil Matters’). Despite its title, most of Possion’s book was a development of ‘probability calculus’, and according to the historian of probability, Ivo Schneider, after its publication “there was hardly anything left that could justify a young mathematician from taking up probability theory”. The heart of Recherches was a single chapter on determining the probability of someone being convicted in a court, by a majority of twelve jurors, each of whom is “is subject to a given probability of not being wrong” and taking into account the police’s assessment of the accused’s guilt. In order to answer this problem, Poisson needed to understand what has become known as the ‘Law of Rare Events’, in contrast to the Law of Large Numbers. Poisson’s starting point was the Binomial Model, based on two possible outcomes such as the toss of a coin, or the establishment of innocence or guilt. De Moivre had considered what would happen as the number of steps in the ‘random walk’ of the Binomial Model became very large, with the probability of a success being about half. Poisson considered what would happen if, as the number of steps increased, the chance of a success decreased simultaneously, so that it became very small.
On this basis, Poisson worked out that if the rate of a rare events occurring, the number of wins per round, was r, then the chance of there being k wins in n rounds was given by
I argue that at the heart of financial economics is not growth but reciprocity, so how do I account for interest?
In 1837 Poisson wrote Recherches sur la probabilité des jugements en matiére criminelle et en matiére civile (‘Research on the Probability of Judgments in Criminal and Civil Matters’). Despite its title, most of Possion’s book was a development of ‘probability calculus’, and according to the historian of probability, Ivo Schneider, after its publication “there was hardly anything left that could justify a young mathematician from taking up probability theory”. The heart of Recherches was a single chapter on determining the probability of someone being convicted in a court, by a majority of twelve jurors, each of whom is “is subject to a given probability of not being wrong” and taking into account the police’s assessment of the accused’s guilt. In order to answer this problem, Poisson needed to understand what has become known as the ‘Law of Rare Events’, in contrast to the Law of Large Numbers. Poisson’s starting point was the Binomial Model, based on two possible outcomes such as the toss of a coin, or the establishment of innocence or guilt. De Moivre had considered what would happen as the number of steps in the ‘random walk’ of the Binomial Model became very large, with the probability of a success being about half. Poisson considered what would happen if, as the number of steps increased, the chance of a success decreased simultaneously, so that it became very small.
On this basis, Poisson worked out that if the rate of a rare events occurring, the number of wins per round, was r, then the chance of there being k wins in n rounds was given by
the Poisson distribution. Apart from being one of
the key models in probability, along with the Binomial and the
Normal, the Poisson distribution has an important financial
interpretation.
E[loan] = X0e-rT.
Consider a banker
lending a sum of money, X0. The banker is concerned
that the borrower does not default, which is hopefully a rare event,
and will eventually pay back the loan. Say the banker assesses that
the borrower will default at a rate of r defaults a day, and
the loan will last T days. The banker might also assume that
they will get all their money back, providing the borrower makes no
defaults in the T days, and nothing if the borrower makes one
or more defaults. On this basis the bankers mathematical expectation
of the value of the loan is
E[loan] = (Probability of no defaults × X0) + (Probability at least one default × 0)
we can ignore the second expression,
since it is zero, and for the first, using the Law of Rare Events, the probability of no defaults is given when k = 0 we have that (rT)0
= 1 and 0! = 1, so
E[loan] = X0e-rT.
So the banker is handing over X0
with the expectation of only getting X0e-rT
< X 0 back. To make the initial loan
amount equal the expected repayment, the banker needs to inflate the
expected repayment by erT ,
That is, the repayment amount needs to be
We can interpret interest in two ways, as a means of "growing" ones wealth, which would be usurious in the Scholastic sense, or as a compensation. If it is a compensation the wealth is not expected to grow, that is, Piketty's whole argument becomes somewhat meaningless.
Michael Northcott argued that the Christian prohibition on usury/interest was related to an intent to inhibit human bondage and he noted that contemporary Islamic finance still prohibited the charging of interest. There in lies a counter argument to the interest equates to slavery claim, it was capitalist Britain that led the way in the emancipation of slavery, Islamic jurisdictions retained slavery into the second half of the twentieth century.
I agree with Michael that usury is a form of bondage, but I do not agree that the charging of interest is usurious, particularly if the interest is determined on the principle of balanced reciprocity. The problem contemporary finance faces is that it emphasising economic growth over social cohesion, the distinction between usury and interest is obscured.
Subscribe to:
Posts (Atom)





